一天一点基础（续1）

wb61850

如图所示，
我们要明确电流的“瞬时值”。
大家看到图片中的“红点”了吗？那个红点所对应的时间以及幅度的值就是电流的瞬时值。
我们可以把波形看成是由很多的“点”组成的，每一个点都有唯一的一组“时间值——幅度值”相对应。

wb61850

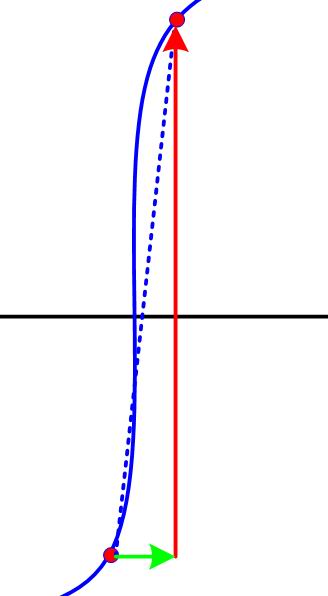
第二，我们要明确电流的“变化率”
首先请大家明确“谁对谁变化”。在这里显然是“电流对时间的变化” 即“电流对时间的变化率”。
如图所示，当有一个时间的增量时（绿色箭头线），就会有一个幅度的增量（红色箭头线）。我们就用幅度的增量与时间的增量的比值表示电流的“增量变化率”单位是安培/秒（A/S）。通俗地讲就是“波形越陡峭的地方它的变化率就越大”。当电流上升时，变化率为正；当电流下降时，变化率为负。
对波形求导数（或微分）其实就是求它的瞬时变化率，不过我们为了说明问题采用了“增量变化率”的概念。

wb61850

wb61850

wb61850

波形的瞬时值和瞬时变化率（在一定的误差范围内也可以用增量变化率近似）是波形的基本特征
当然，还有一些特征值如平均值、有效值等。这方面的资料很多，大家可以查找一下，这里就不一一介绍了

wb61850

真舍不得大家
不过得说“再见”了

wb61850

告诉大家，俺可是有身份的人哦，有啥身份呢？就是有身份证的人呗
http://v.ku6.com/show/-tBU3PhH3LL3NuoI.html

wb61850

共同学习，一起进步！OY、OK、OL

wb61850

大家知道，电感器的VAR和电容器的VAR都是涉及“微积分”关系的
那么我们应该怎样理解“微积分”呢？
我觉得用“图示”的方法更形象些。

wb61850

大家请看上面这张图
我们在理想电感器两端加上一个一定波形的信号电压u(t)，那么就会在电感器中产生相应的电流i(t)。
现在我们通过示波器测量电感电压u(t)和电感电流i(t)，来观察一下它们之间的关系。
需要指出“理想的电感器”是忽略分布电阻、分布电容等因素理想化的电感模型。它在通过一定的电流时，就会在其周围空间建立一定的磁场，因此也就存储了一定的磁场能量。当通过其的电流随时间变化时，磁场也随时间变化，磁场能量也随时间变化。

wb61850

大家知道“电感器的电流i(t)是其电压u(t)对时间的积分”，这一点是与电阻器的VAR本质不同的
下面我们通过“波形”就可以发现这个问题了。

wb61850

大家请看，这就是电感器两端的电压u(t)和电感器电流i(t)的波形了。红色波形是电压u(t)，蓝色波形是电流i(t)。
我们可以发现，它们在形状上是完全不同的
但是，它们的频率是相同的，这点请大家注意。
我们现在取的自变量是电压，因变量是电流。因此我们采用锯齿波电压源来激励电感器，以求得通过其的电流i(t)。

wb61850

定性的讲，对信号波形积分就是求其在一定区间的面积
我们知道，电感电流与电感电压之间是“积分关系”。
既然如此，电感的电流就必然与电感电压对时间的积分有关联的了。

wb61850

如图所示，标尺1和标尺2之间是信号的一个周期时间。由于电压和电流都是同频率的非正弦周期信号，因此研究一个周期内信号的变化即可。
那么我们就看一下在电压u(t)的一个周期内，电流i(t)的变化吧

wb61850

请大家注意，标尺之间的电压（红色）所包围的“三角形”面积是随时间增大的，电流随时间的增大正是反映这点。

wb61850

标尺2到了图中的这个时间位置时，两个“红边三角形”的面积恰好相等，不过它们的符号相反（电压进入负半周时三角形面积为负）因此面积之和等于零，因此标尺2所在的时间位置电流i(t)的瞬时值也等于零。

wb61850

wb61850

如上图所示，标尺2到了这个时刻，“负的红边三角形”的面积最大，电感电流i(t)也到达负的最大值

wb61850

  当标尺2到了信号的一个周期的时间时，两个极性相反的三角形的面积又相等了，因此电流i(t)=0

wb61850

以上就是“电感瞬时电流是电感电压对时间的积分”的图示意义
说明电感电流的瞬时值不仅仅决定于当前的电压值，而且决定于当前时间以前的所有时间的电压值（电压波形的时间积分）。或者说，决定于“电压的全部历史”。